library(nmmr)
library(tidyr)
library(ggplot2)
library(dplyr)
#> 
#> Attaching package: 'dplyr'
#> The following objects are masked from 'package:stats':
#> 
#>     filter, lag
#> The following objects are masked from 'package:base':
#> 
#>     intersect, setdiff, setequal, union
library(forcats)

set.seed(1234)

Fitting a the main Bayesian model is comparable to the Bayesian model presented in vignette('deming-regression'). This vignette additionally walks through how nmmr can be used to compare two models.

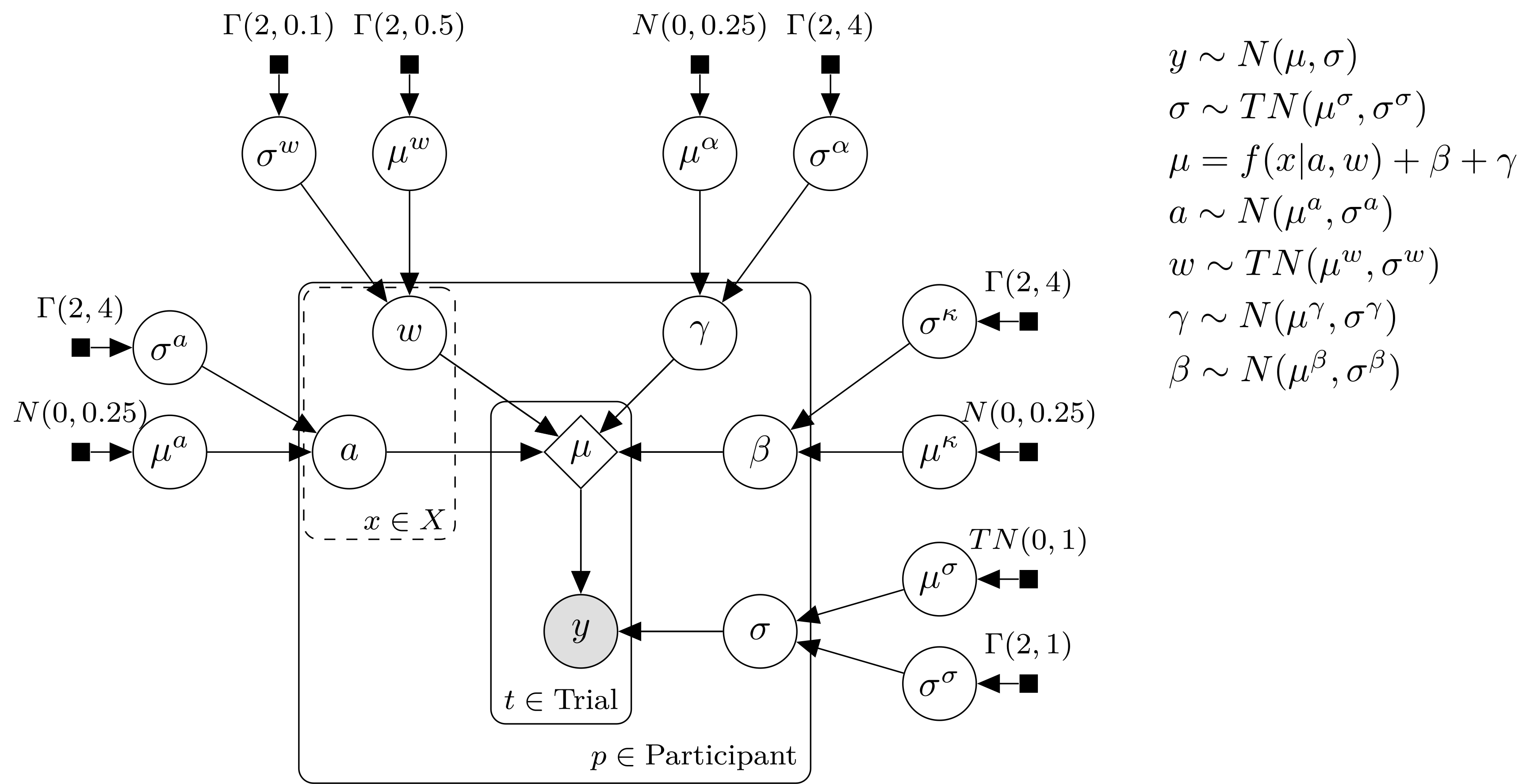
$Schematic of the Bayesian model. Filled square nodes indicate priors, open circles are estimated parameters, the shaded circles are observed data, and the open diamond is the result of a deterministic function of the parameters. Nodes are grouped with the square "plates", indicating over which subsets of the data the node is replicated. The distribution assigned to each node is listed to the right of the diagram. $N(\mu,\sigma)$ is a normal with location $\mu$ and scale $\sigma$, and $TN(\mu,\sigma)$ is a normal with the same parameters, truncated below at $\mu$. Each equation in the upper right is associated with an arrow in the diagram, describing a relationship between nodes.$

Schematic of the Bayesian model. Filled square nodes indicate priors, open circles are estimated parameters, the shaded circles are observed data, and the open diamond is the result of a deterministic function of the parameters. Nodes are grouped with the square “plates”, indicating over which subsets of the data the node is replicated. The distribution assigned to each node is listed to the right of the diagram. $N(\mu,\sigma)$ is a normal with location $\mu$ and scale $\sigma$, and $TN(\mu,\sigma)$ is a normal with the same parameters, truncated below at $\mu$. Each equation in the upper right is associated with an arrow in the diagram, describing a relationship between nodes.

Run Model

These models require a long time to run. To speed things along for this vignette, the dataset is reduced to just three voxels

small <- sub02 %>%
  group_by(orientation, run, ses) %>%
  slice_head(n = 10) %>%
  mutate(voxel = fct_drop(voxel)) %>%
  ungroup()

Next, initialize two versions of the model.

model_multiplicative <- Model$new(small, form = "multiplicative")
model_additive <- Model$new(small, form = "additive")


# fewer samples run for the sake of a quicker vignette
# In a real analysis, you would probably want at least 4 chains with 
# 1000 samples each
fit_multiplicative <- model_multiplicative$sample(
  chains = 2, 
  parallel_chains = 2, 
  seed = 1,
  iter_sampling = 100,
  iter_warmup = 500)
#> Running MCMC with 2 parallel chains...
#> 
#> Chain 1 Iteration:   1 / 600 [  0%]  (Warmup)
#> Chain 1 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:
#> Chain 1 Exception: normal_lpdf: Location parameter is inf, but must be finite! (in '/tmp/RtmpuEnmDU/model-a74f4526b396.stan', line 43, column 2 to column 41)
#> Chain 1 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,
#> Chain 1 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.
#> Chain 1
#> Chain 1 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:
#> Chain 1 Exception: normal_lpdf: Location parameter[8] is -nan, but must be finite! (in '/home/runner/work/nmmr/nmmr/inst/stan/model/likelihood.stan', line 24, column 4, included from
#> Chain 1 '/tmp/RtmpuEnmDU/model-a74f4526b396.stan', line 69, column 0)
#> Chain 1 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,
#> Chain 1 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.
#> Chain 1
#> Chain 2 Iteration:   1 / 600 [  0%]  (Warmup)
#> Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:
#> Chain 2 Exception: normal_lpdf: Location parameter is inf, but must be finite! (in '/tmp/RtmpuEnmDU/model-a74f4526b396.stan', line 43, column 2 to column 41)
#> Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,
#> Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.
#> Chain 2
#> Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:
#> Chain 2 Exception: normal_lpdf: Location parameter[577] is inf, but must be finite! (in '/home/runner/work/nmmr/nmmr/inst/stan/model/likelihood.stan', line 24, column 4, included from
#> Chain 2 '/tmp/RtmpuEnmDU/model-a74f4526b396.stan', line 69, column 0)
#> Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,
#> Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.
#> Chain 2
#> Chain 1 Iteration: 100 / 600 [ 16%]  (Warmup) 
#> Chain 2 Iteration: 100 / 600 [ 16%]  (Warmup)
#> Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:
#> Chain 2 Exception: normal_lpdf: Location parameter[584] is -nan, but must be finite! (in '/home/runner/work/nmmr/nmmr/inst/stan/model/likelihood.stan', line 24, column 4, included from
#> Chain 2 '/tmp/RtmpuEnmDU/model-a74f4526b396.stan', line 69, column 0)
#> Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,
#> Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.
#> Chain 2
#> Chain 1 Iteration: 200 / 600 [ 33%]  (Warmup) 
#> Chain 2 Iteration: 200 / 600 [ 33%]  (Warmup) 
#> Chain 1 Iteration: 300 / 600 [ 50%]  (Warmup) 
#> Chain 2 Iteration: 300 / 600 [ 50%]  (Warmup) 
#> Chain 2 Iteration: 400 / 600 [ 66%]  (Warmup) 
#> Chain 1 Iteration: 400 / 600 [ 66%]  (Warmup) 
#> Chain 1 Iteration: 500 / 600 [ 83%]  (Warmup) 
#> Chain 1 Iteration: 501 / 600 [ 83%]  (Sampling) 
#> Chain 2 Iteration: 500 / 600 [ 83%]  (Warmup) 
#> Chain 2 Iteration: 501 / 600 [ 83%]  (Sampling) 
#> Chain 1 Iteration: 600 / 600 [100%]  (Sampling) 
#> Chain 1 finished in 3.8 seconds.
#> Chain 2 Iteration: 600 / 600 [100%]  (Sampling) 
#> Chain 2 finished in 4.1 seconds.
#> 
#> Both chains finished successfully.
#> Mean chain execution time: 3.9 seconds.
#> Total execution time: 4.2 seconds.

fit_additive <- model_additive$sample(
  chains = 2, 
  parallel_chains = 2, 
  seed = 1,
  iter_sampling = 100,
  iter_warmup = 500)
#> Running MCMC with 2 parallel chains...
#> 
#> Chain 1 Iteration:   1 / 600 [  0%]  (Warmup)
#> Chain 1 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:
#> Chain 1 Exception: normal_lpdf: Location parameter is inf, but must be finite! (in '/tmp/RtmpuEnmDU/model-a74f4526b396.stan', line 43, column 2 to column 41)
#> Chain 1 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,
#> Chain 1 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.
#> Chain 1
#> Chain 2 Iteration:   1 / 600 [  0%]  (Warmup)
#> Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:
#> Chain 2 Exception: normal_lpdf: Location parameter is inf, but must be finite! (in '/tmp/RtmpuEnmDU/model-a74f4526b396.stan', line 43, column 2 to column 41)
#> Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,
#> Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.
#> Chain 2
#> Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:
#> Chain 2 Exception: normal_lpdf: Location parameter[145] is -nan, but must be finite! (in '/home/runner/work/nmmr/nmmr/inst/stan/model/likelihood.stan', line 24, column 4, included from
#> Chain 2 '/tmp/RtmpuEnmDU/model-a74f4526b396.stan', line 69, column 0)
#> Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,
#> Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.
#> Chain 2
#> Chain 1 Iteration: 100 / 600 [ 16%]  (Warmup) 
#> Chain 2 Iteration: 100 / 600 [ 16%]  (Warmup)
#> Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:
#> Chain 2 Exception: normal_lpdf: Location parameter[1] is -nan, but must be finite! (in '/home/runner/work/nmmr/nmmr/inst/stan/model/likelihood.stan', line 24, column 4, included from
#> Chain 2 '/tmp/RtmpuEnmDU/model-a74f4526b396.stan', line 69, column 0)
#> Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,
#> Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.
#> Chain 2
#> Chain 1 Iteration: 200 / 600 [ 33%]  (Warmup) 
#> Chain 2 Iteration: 200 / 600 [ 33%]  (Warmup) 
#> Chain 1 Iteration: 300 / 600 [ 50%]  (Warmup) 
#> Chain 2 Iteration: 300 / 600 [ 50%]  (Warmup) 
#> Chain 1 Iteration: 400 / 600 [ 66%]  (Warmup) 
#> Chain 2 Iteration: 400 / 600 [ 66%]  (Warmup) 
#> Chain 1 Iteration: 500 / 600 [ 83%]  (Warmup) 
#> Chain 1 Iteration: 501 / 600 [ 83%]  (Sampling) 
#> Chain 2 Iteration: 500 / 600 [ 83%]  (Warmup) 
#> Chain 2 Iteration: 501 / 600 [ 83%]  (Sampling) 
#> Chain 1 Iteration: 600 / 600 [100%]  (Sampling) 
#> Chain 1 finished in 2.7 seconds.
#> Chain 2 Iteration: 600 / 600 [100%]  (Sampling) 
#> Chain 2 finished in 2.9 seconds.
#> 
#> Both chains finished successfully.
#> Mean chain execution time: 2.8 seconds.
#> Total execution time: 2.9 seconds.

As with any Bayesian analysis, you should be wary about convergence issues. See vignette('deming-regression') for a discussion on how to check the output of the model.

Note that, in this reduced example where there are only 10 voxels, the models will likely have convergence issues¹.

Compare Models

Assuming that the posterior was estimated accurately, they may now be used for model comparison. In the original report, models were compared based on their predictive abilities, based on an efficient approximation to leave-one-out cross-validation. To implement this, nmmr takes advantage of functions provided by the loo package. The first step involves using a $loo() method to calculate the expected log pointwise predictive density (ELPD).

elpd_multiplicative <- fit_multiplicative$loo(cores = 2)
elpd_additive <- fit_additive$loo(cores = 2)

The ELPD is closely related to information criteria like the AIC, BIC, or WAIC, but the ELPD requires fewer assumptions and is has more diagnostics for checking when the value should be questioned. For further details, see help("loo-glossary", package="loo").

The output of the $loo() method is an object that has class psis_loo (see ?loo::loo), and so the diagnostics provided by the loo package are available. At a minimum, the object should be printed, and the k values should be inspected. Values of k larger than 0.7 are suspect, and indicate that the model comparison score cannot be trusted.

elpd_multiplicative
#> 
#> Computed from 200 by 1440 log-likelihood matrix
#> 
#>          Estimate   SE
#> elpd_loo  -2737.9 32.7
#> p_loo        35.9  2.0
#> looic      5475.7 65.5
#> ------
#> Monte Carlo SE of elpd_loo is 0.6.
#> 
#> Pareto k diagnostic values:
#>                          Count Pct.    Min. n_eff
#> (-Inf, 0.5]   (good)     1429  99.2%   11        
#>  (0.5, 0.7]   (ok)         11   0.8%   45        
#>    (0.7, 1]   (bad)         0   0.0%   <NA>      
#>    (1, Inf)   (very bad)    0   0.0%   <NA>      
#> 
#> All Pareto k estimates are ok (k < 0.7).
#> See help('pareto-k-diagnostic') for details.

In this case, there were only a few voxels, and so the diagnostics indicate trouble. With more data, the diagnostics will likely improve.

For a full list of the diagnostics, see help("pareto-k-diagnostic", package="loo").

If the diagnostics look okay, ten the model may be compared.

loo::loo_compare(elpd_multiplicative, elpd_additive)
#>        elpd_diff se_diff
#> model1  0.0       0.0   
#> model2 -7.2       2.4

Higher scores are better. The winning model will always have an elpd_diff (ELPD difference) of 0, and the other models will be compared to this winner. A second column gives the standard error of the difference (e.g., for determining whether any difference is “reliable”). For details, see ?loo::loo_compare.

For an expanded discussion on why, see https://betanalpha.github.io/assets/case_studies/identifiability.html, and https://betanalpha.github.io/assets/case_studies/hierarchical_modeling.html ↩︎

vtf

Run Model

Compare Models