Many cognitive experiments involve asking participants to answer questions that require circular responses (Figure 1). What was the color of the shape you just saw? In which direction was the arrow pointing? How tilted was the bar? The answers required by these questions differ fundamentally from the more common, categorical responses required to questions. Was the color green or red? Was the arrow pointing left or right? Was the bar tilted more than 45 degrees from vertical, between 45-90, or more than 90 degrees? In the continuous case, the experimenter looses the ability to classify responses as either correct or incorrect, and an analysis must consider participants’ degree of inaccuracy, their relative error. Circularity adds the additional complication that a response can only be erroneous up to a point; if a person responds that a vertical bar is 3 degrees offset from vertical on trial one and 359 degrees on trial two, the analysis must acknowledge that the average is close to truth. Although many models exist that describe how a participant will respond when the choice is binary, models of these are much more limited.

Figure 1: Cognitive experiments often require participants to provide a circularly continuous response. A participant might be asked to study shapes of different colors, hold the colors of every shape in memory, and then report on the one shape’s color.

Smith (2016) present a new model of how participants provide circularly continuous responses, called the circular diffusion model. It is a model of the decision-making process, analyzing both the numerical value participants provided and how long it took them to provide a response. The model extends the drift diffusion model of binary decisions (Ratcliff 1978). Like the drift diffusion model, the circular diffusion model casts perceptual decisions as a stochastic process of evidence accumulation to a threshold; evidence is accumulated over time, and when enough evidence has been reached the process terminates in a motor behavior. The model is not concerned with how evidence accumulates, just that it does. In a working memory experiment, evidence might accumulate through repeated probes of memory. In a perceptual-decision task, each saccade might provide a different amount of evidence. In both cases, evidence grows at an average rate, and when there is enough evidence for a decision that decision is made. The amount of time required to reach that threshold of evidence is the response time. The circular diffusion model, therefore, proposes that the responses of rapid decisions which require circularly continuous responses can be modeled as a particle drifting in two dimensions out towards a circular boundary.

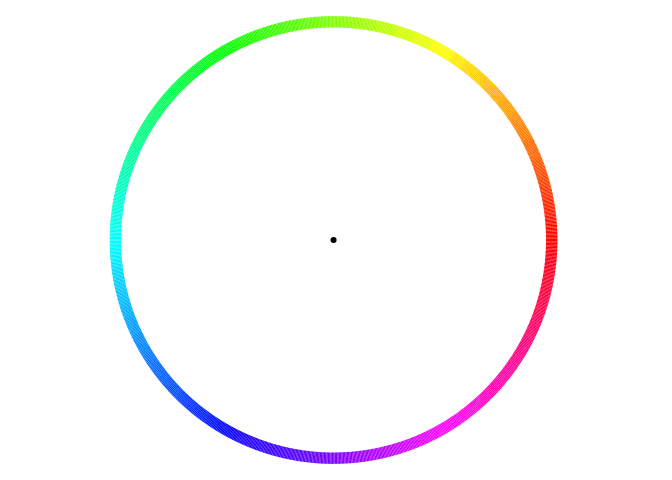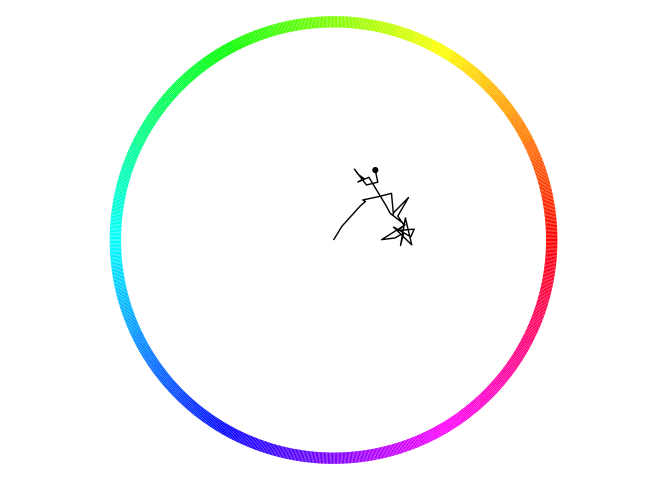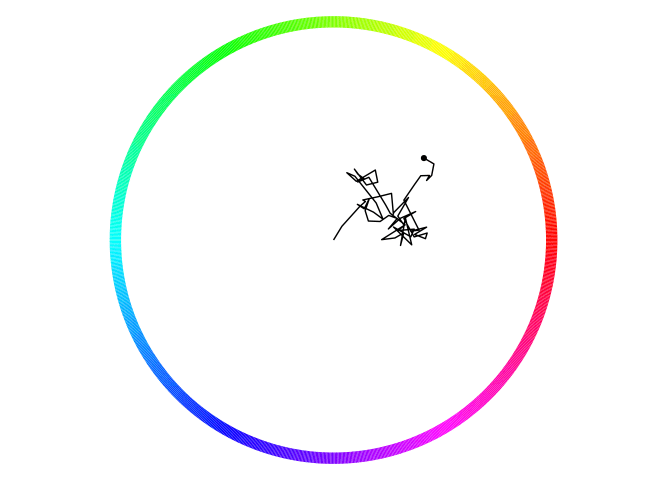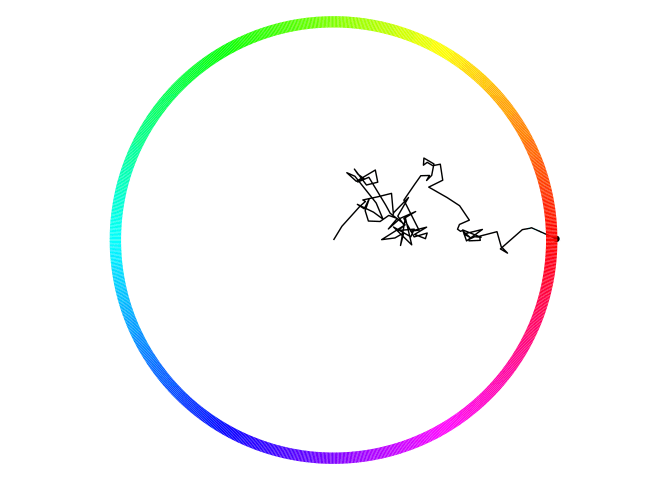
Figure 2: A diffusing particle models perceptual decisions. In this example, wherever the particle first crosses the circle corresponds to the response, and the amount of time required to reach the edge is their response time.

Using the circular diffusion model affords researchers the same advantages conferred by using the standard drift diffusion model: the decision-making process can be decomposed into parameters of the model, and those parameters have psychologically meaningful values. For example, a participant might respond quickly, but that could either occur because they accumulate evidence rapidly or because they set a low threshold for evidence. There are three key parameters in the model: 1) the average direction the particle drifts (towards what decision are participants mostly accumulating evidence?), 2) the average rate at which the particle drifts (how quickly do participants accumulate evidence?), and 3) the radius of the circular boundary (how conservative are participants?). Estimating these parameters for participants across different conditions of an experiment enables the researcher to “measure” each of these psychological constructs given participants’ behavior.